Question

A newsletter publisher believes that 55% of their readers own a Rolls Royce. Is there sufficient evidence at the 0.05 level to refute the publisher's claim? State the null and alternative hypotheses for the above scenario.

Answer 1

Set up hypotheses:

The null hypotheses is that the proportion of readers who own a Rolls Royce is equal to 0.55

Null hypotheses = H₀: p = 0.55

The alternate hypotheses is that the proportion of readers who own a Rolls Royce is not equal to 0.55

Alternate hypotheses = H₁: p ≠ 0.55

Determine the type of test:

Since the alternate hypothesis states that the proportion of readers who own a Rolls Royce is different, therefore it is a two-tailed test.

Determine the level of significance and Critical Z-score:

Given level of significance = 0.05

Since it is a two-tailed test,

Z-score = 1.960 (two tailed)

Set up decision rule:

Since it is a two-tailed test, using a Z statistic at a significance level of 5%

We Reject H₀ if Z < -1.960 or Z > 1.960

We Reject H₀ if p ≤ α

Compute the test statistic:

The test statistic may be calculated using,

`$ Z = \frac{\hat{p} - p}{ \sqrt{(p(1-p))/(n) }} $`

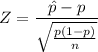
We are not given enough information to find out the test statistic.

Conclusion:

We do not have enough information to accept or refuse the publisher's claim.