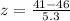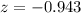Question

Jenna drives on average 46 miles per day with a standard deviation of 5.3 miles per day. Suppose Jenna's miles driven per day are normally distributed. Let X = the number of miles driven in a given day. Then X - N(46, 5.3). If necessary, round to three decimal places.

Provide your answer below:
Suppose Jenna drives 41 miles on Monday. The Z-score when x - 41 is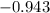______ . The mean is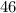________ This z-score tells you that x = 41 is________ standard deviations to the left of the mean.

Answer 1

Suppose Jenna drives 41 miles on Monday. The Z-score when x - 41 is
`-0.943`. The mean is
`46` This z-score tells you that x = 41 is
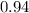`0.94` standard deviations to the left of the mean.

Explanation:

From the question we are told that

The mean is
`\= x = 46\ miles / day`

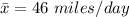
The standard deviation is
`\sigma = 5.3 \ miles \ per \ day`

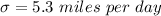
The value of = 41

Generally the z-score is mathematically represented as

`z = (x-\= x)/(\sigma )`

substituting values

`z = (41-46)/(5.3)`

`z = - 0.943`