Question

A Ferris wheel is 15 meters in diameter and boarded from a platform that is 1 meters above the ground. The six o'clock position on the Ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 2 minutes. How many minutes of the ride are spent higher than 15 meters above the ground?

Answer 1

The number of minutes of the ride that are spent higher than 15 meters above the ground is 18 minutes.

Explanation:

We will use the sin function for the height of the Ferris wheel.

`y=A\ sin(B(x+C))+D`

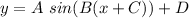
A = amplitude

C = phase shift

D = Vertical shift

2π/B = period

From the provided information:

A = 15/2 = 7.5 m

`Period=2\\\\(2\pi)/(B)=2\\\\B=\pi`

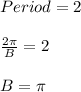
Compute the Vertical shift as follows:

D = A + Distance of wheel from ground

= 7.5 + 1

= 8.5

The equation of height is:

`h(t)=7.5\cdot sin(\pi (t+C))+8.5`

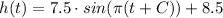
Now at t = 0 the height is, h (t) = 1 m.

Compute the value of C as follows:

`h(t)=7.5\cdot sin(\pi (t+C))+8.5`

`1=7.5\cdot sin(\pi (0+C))+8.5\\\\-7.5=7.5\cdot sin\ \pi C\\\\sin\ \pi C=-1\\\\\pi C=sin^(-1)(-1)\\\\\pi C=(3\pi)/(2)\\\\C=(3)/(2)`

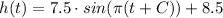
So, the complete equation of height is:

`h(t)=7.5\cdot sin(\pi (t+(3)/(2)))+8.5`

Compute the number of minutes of the ride that are spent higher than 15 meters above the ground as follows:

h (t) ≥ 15

`h(t)=15\\\\7.5\cdot sin(\pi (t+(3)/(2)))+8.5=15\\\\7.5\cdot sin(\pi (t+(3)/(2)))=6.5\\\\sin(\pi (t+(3)/(2)))=(6.5)/(7.5)\\\\(\pi (t+(3)/(2)))=sin^(-1)[(13)/(15)]\\\\\pi (t+(3)/(2))=60.074\\\\t+(3)/(2)=19.122\\\\t=17.622\\\\t\approx 18`

Thus, the number of minutes of the ride that are spent higher than 15 meters above the ground is 18 minutes.