Question

A triangle in the xy-coordinate plane is formed by the points (3, 5), (− 1, 5) , and (3,− 6) . What is the perimeter and area of this triangle?

Answer 1

Therefore, the perimeter of the triangle is 26.7 units and the area is 22 square units.

Explanation:

Given the vertices of a triangle as: A(3, 5), B(− 1, 5), and C(3,− 6)

Since A and B are on the same y-coordinate, we have that:

AB = 3-(-1)=4 Units

Since A and C are on the same x-coordinate, we have that:

AC=5-(-6)=11 Units

Next, we determine the distance BC using the distance formula.

Given: B(− 1, 5), and C(3,− 6)

`BC=√((3-(-1))^2+(-6-5)^2)\\= √((4)^2+(-11)^2)=√(137)$ Units`

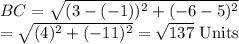
Therefore:

Perimeter of the Triangle

`= 4+11+√(137)\\ =15+√(137)$ Units\\=26.7 Units`

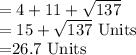
On plotting the triangle, it forms a right triangle such that the:

Base = 4 Units

Height = 11 Units

Therefore:

Area of a triangle
`=\frac12 *Base*Height`

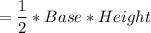
Therefore:

Area of the Triangle = 0.5 X 4 X 11

=22 Square Units.

Therefore, the perimeter of the triangle is 26.7 units and the area is 22 square units.