Question

Complete the square to rewrite y-x^2-6x+14 in vertex form. then state whether the vertex is a maximum or minimum and give its cordinates

Answer 1

`y= x^2 -6x +((6)/(2))^2 +14 -((6)/(2))^2`

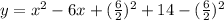
And solving we have:

`y= x^2 -6x +9 + 14 -9`

`y= (x-3)^2 +5`

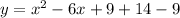
And we can write the expression like this:

`y-5 = (x-3)^2`

The vertex for this case would be:

`V= (3,5)`

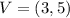
And the minimum for the function would be 3 and there is no maximum value for the function

Explanation:

For this case we have the following equation given:

`y= x^2 -6x +14`

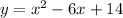
We can complete the square like this:

`y= x^2 -6x +((6)/(2))^2 +14 -((6)/(2))^2`

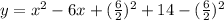
And solving we have:

`y= x^2 -6x +9 + 14 -9`

`y= (x-3)^2 +5`

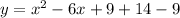
And we can write the expression like this:

`y-5 = (x-3)^2`

The vertex for this case would be:

`V= (3,5)`

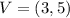
And the minimum for the function would be 3 and there is no maximum value for the function