Answer:
The correct answer is First option:
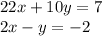
Explanation:
We are given 4 equations:
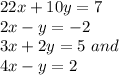
Let us solve the first two:

Multiplying (2) with 10 and adding to (1):
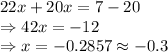
So, approximately, value of x is -0.3.
Putting value of x in (2):
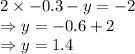
value of x is approximately -0.3 so y is approximately 1.4.
So, the solution is
 (–0.3, 1.4)
(–0.3, 1.4)
The correct answer is First option:
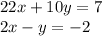
The above two equations have a solution approximately (–0.3, 1.4).