Question

Can someone help me solve (a) and (c) pls.
Thanks ​

Answer 1

Area of ABCD = 959.93 units²

Explanation:

a). By applying Sine rule in the ΔABD,

`\frac{\text{SinA}}{46}=\frac{\text{Sin}\angle{DBA}}{35}`

`\frac{\text{Sin110}}{46}=\frac{\text{Sin}\angle{DBA}}{35}`

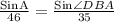
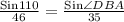
Sin∠DBA =
`\frac{35* \text{Sin}(110)}{46}`

m∠DBA =
`\text{Sin}^(-1)(0.714983)`

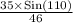
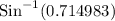
m∠DBA = 45.64°

Therefore, m∠ADB = 180° - (110° + 45.64°) = 24.36°

m∠ADB = 24.36°

c). Area of ABCD = Area of ΔABD + Area of ΔBCD

Area of ΔABD = AD×BD×Sin(
`(24.36)/(2)`)

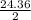= 35×46Sin(12.18)

= 339.68 units²

Area of ΔBCD = BD×BC×Sin(
`(59.92)/(2)`)°

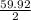= 46×27×(0.4994)

= 620.25 units²

Area of ABCD = 339.68 + 620.25

= 959.93 units²