Answer:
At a significance level of 0.1 (90% reliability), there is not enough evidence to support the claim that there is significant difference in mean mineral deposits in the two holes.
Explanation:
This is a matched-pair t-test for the difference.
We have to calculate the difference d for each pair, and then treat his as the sample for our test.
For example, the difference for the first pair is:
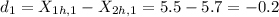
Then, the sample for the differences between each pair is:
![d=[-0.2 , -0.2 , -0.1 , 2.6 , 0.7 , 0.9 , 1.7 , -1.6 , 1 , 1.1 , -1.7 , -0.3 , 0.1 , -1.5 , -1.2]](https://img.qammunity.org/2021/formulas/mathematics/college/lrbgssij1o793zrbmfgk4a0dt1n85ik7lt.png)
The sample mean and standard deviation are:

The claim is that there is significant difference in mean mineral deposits in the two holes.
Then, the null and alternative hypothesis are:
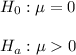
The significance level is 0.1.
The sample has a size n=15.
The sample mean is M=0.09.
As the standard deviation of the population is not known, we estimate it with the sample standard deviation, that has a value of s=1.26.
The estimated standard error of the mean is computed using the formula:
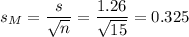
Then, we can calculate the t-statistic as:
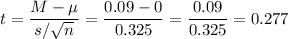
The degrees of freedom for this sample size are:

This test is a right-tailed test, with 14 degrees of freedom and t=0.277, so the P-value for this test is calculated as (using a t-table):
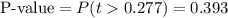
As the P-value (0.393) is bigger than the significance level (0.1), the effect is not significant.
The null hypothesis failed to be rejected.
At a significance level of 0.1, there is not enough evidence to support the claim that there is significant difference in mean mineral deposits in the two holes.