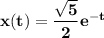Answer:
Explanation:
Given that:
mass of the object = 2 kg
A force of 5nt is applied to move the object 0.5m from its equilibrium position.
i.e
Force = 5 newton
Stretchin (x) =0.5 m
Damping force = 1 newton
Velocity = 0.25 m/second
The object is pulled to the left until the spring is stretched lm and then released with the initial velocity of 2m/second to the right
SOLUTION:
If F = kx
Then :
5 N = k(0.5 m)
where ;
k = spring constant.
k = 5 N/0.5 m
k = 10 N/m
the damping force of the object sliding on the table is 1 newton when the velocity is 0.25m/second.
SO;
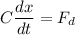
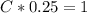
C =
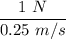
C = 4 Ns/m
NOW;
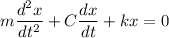
Divide through by m; we have;
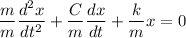
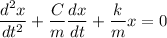
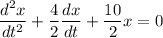
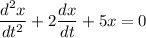
we all know that:
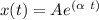 ------ (1)
------ (1)
SO;
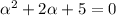
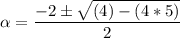

Thus ;
![x(t) = e^(-t)[A \sin (2t)+ B cos (2t)]](https://img.qammunity.org/2021/formulas/mathematics/college/1n4z2o0dx1susx944n7i5zyrledumjxskw.png) ------------ (1)
------------ (1)
However;
![(dx)/(dt) = e^(-t)[A \sin (2t)+ B cos (2t)]+ 2e ^(-t) [A \cos (2t)- B \ Sin (2t)]](https://img.qammunity.org/2021/formulas/mathematics/college/rq7dngqzu5q09213p1wa6wrhhne27qt3ss.png) ------- (2)
------- (2)
From the question ; we are being told that;
The object is pulled to the left until the spring is stretched 1 m and then released with the initial velocity of 2m/second to the right.
So ;
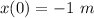
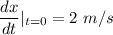
x(0) ⇒ B = -1
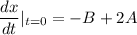
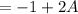
1 = 2A
A =

From (1)
![x(t) = e^(-t)[A \sin (2t)+ B cos (2t)]](https://img.qammunity.org/2021/formulas/mathematics/college/1n4z2o0dx1susx944n7i5zyrledumjxskw.png)
![x(t) = e^(-t)[(1)/(2) \sin (2t)+ (-1) cos (2t)]](https://img.qammunity.org/2021/formulas/mathematics/college/97u8oml6fd4fwzf3hv6osu88axls9obd3b.png)
![x(t) = e^(-t)[(1)/(2) \sin (2t)-cos (2t)]](https://img.qammunity.org/2021/formulas/mathematics/college/hax78skoh9yedhc6how6tcks9p48tjp9ky.png)
Assuming;


Therefore:

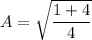
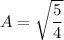
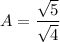
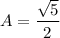
where;
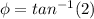
Therefore;
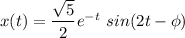
From above ; the amplitude is ;