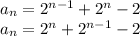Answer:
A)
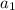 = 1,
= 1,
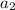 = 4
= 4
B)
 = 2
= 2
 + 2
+ 2
C)
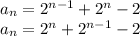
Explanation:
For n ≥ 1 ,
S is a set containing 2^n distinct real numbers
an = no of comparisons to be made between pairs of elements of s
A)
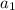 = no of comparisons in set (s)
= no of comparisons in set (s)
that contains 2 elements = 1
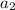 = no of comparisons in set (s) containing 4 = 4
= no of comparisons in set (s) containing 4 = 4
B) an = 2a
 + 2
+ 2
C) using the recurrence relation
a
 = 2a
= 2a
 + 2
+ 2
substitute the following values 2,3,4 .......... for n
a
 = 2a
= 2a
 + 2
+ 2
a
 = 2a
= 2a
 + 2 =
+ 2 =
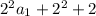
a
 =
=
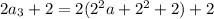
=
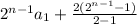 ---------------- (x)
---------------- (x)
since 2^1 + 2^2 + 2^3 + ...... + 2^n-1 =
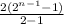
applying the sum formula for G.P
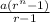
Note ; a = 2, r =2 , n = n-1
a1 = 1
so equation x becomes