Answer:
The magnitude of the magnetic force on this proton would be approximately
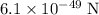 .
.
The direction of the magnetic force on this proton will point to the east.
Step-by-step explanation:
(a)
Let
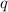 denote the size of the charge. Let
denote the size of the charge. Let
 denote the velocity of this charge. Let
denote the velocity of this charge. Let
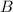 denote the strength of a uniform magnetic field. Assume that this charge is moving through this magnetic field. Let the angle between
denote the strength of a uniform magnetic field. Assume that this charge is moving through this magnetic field. Let the angle between
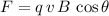 .
.
The direction of the velocity of the proton in this question is horizontal. On the other hand, the magnetic field in this question is oriented vertically. As a result, the angle between the
 and the
and the
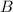 here would be
here would be
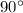 .
.
Look up the size of the charge on a proton (the elementary charge) in Coulombs:
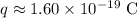 .
.
Apply this formula to find the magnitude of the magnetic force on this proton:
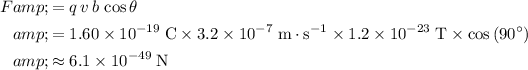 .
.
(b)
Apply the right-hand rule to determine to direction of this magnetic force. There are more than one variations of this rule. Here's one of them:
- Start by stretching out all five fingers on the right hand in the direction of the motion of this proton (the positive charge, to the north in this question.)
- Rotate the right arm, so that the imaginary magnetic field lines enter from the back of the right hand and exits from the palm (perpendicularly.)
- Stretch out the thumb on the right hand so that it points at a
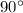 with the right index finger. The thumb should now point in the direction of the magnetic force on this proton.
with the right index finger. The thumb should now point in the direction of the magnetic force on this proton.