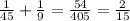Question

In how many different ways can 2/15 be represented as 1/a+1/b, if a and b are positive integers with a greater than or equal to b?

Answer 1

There are three possible combinations of positive integers such that a > b:

(1) a = 15 and b = 15

(2) a = 20 and b = 12

(3) a = 45 and b = 9

Explanation:

Notice that the possible factors (different from "1") of the denominator "15" are: 3, 5, and 15.

The answer for the case a = 15 and b = 15 is obvious since :

`(1)/(15) + (1)/(15) = (2)/(15)`

Then the possibility of a multiple of 5 for one of the denominators (let's say 5*n) and a multiple of 3 (let's say 3*m)for the other one gives the general equation:

`(1)/(5n) +(1)/(3m) =(2)/(15)`

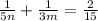
which should verify the following as we try to solve for one of the unknowns multiplicative factors which by the way have to be positive for the requirement given in the problem:

`(5n+3m)/(15mn) =(2)/(15)\\(5n+3m)/(mn) =(2)/(1)\\5n+3m=2mn\\(5n+3m)/(mn) =2\\(5)/(m) +(3)/(n) =2\\(5)/(m)=2-(3)/(n)`

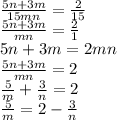
This last equation is very simple to analyze using integer values for "n" which would render a positive value on the right hand side, and then check from that set the ones that give an integer for the value "m".

Those found were:

For n=3, and m=5, a=15, and b=15 (the obvious solution discussed above)

`(1)/(15) +(1)/(15)=(2)/(15)`

For n = 4 and m = 4, a = 20, and b = 12

`(1)/(20) +(1)/(12)=(32)/(240)=(2)/(15)`

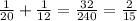
and for n=9 and m=3, a=45 and b = 9

`(1)/(45) +(1)/(9)=(54)/(405)=(2)/(15)`