Answer:
Because the product is always non-termination,non-repeating decimal.
Explanation:
If we have
 is irrational;
is irrational;
 is rational such that
is rational such that
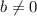 , then
, then
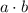 is irrational.
is irrational.
A way to represent this is:
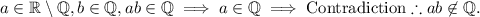
Note that we have a contradiction, because
 is not a rational number, as I stated in the beginning. Therefore, ab is irrational.
is not a rational number, as I stated in the beginning. Therefore, ab is irrational.