Assuming
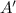 denotes the complement of the set
denotes the complement of the set
 , i.e. all elements in the universal set that do not belong to
, i.e. all elements in the universal set that do not belong to
 , then we can prove this in general.
, then we can prove this in general.
To establish equality between two sets, you need to show that they are both subsets of one another.
- Prove
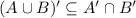 :
:
Let
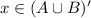 .
.
By definition of set complement, this means
 .
.
By definition of set union,
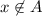 and
and
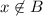 .
.
By definition of complement,
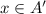 and
and
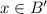 .
.
By definition of set intersection,
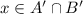 .
.
Therefore
 is a subset of
is a subset of
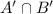 , because membership of some arbitrary element in the first set directly implies membership in the second set.
, because membership of some arbitrary element in the first set directly implies membership in the second set.
- Prove
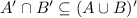 :
:
Let
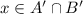 . The proof follows similarly as above.
. The proof follows similarly as above.
By definition of intersection,
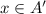 and
and
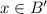 .
.
By definition of complement,
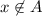 and
and
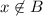 .
.
By definition of union,
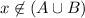 .
.
By definition of complement,
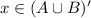 .
.
Therefore
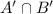 is a subset of
is a subset of
 .
.
And hence both sets are equal, regardless of what the sets may be.