Question

Which of the following describes the transformation of g (x) = 3 (2) Superscript negative x Baseline + 2 from the parent function f (x) = 2 Superscript x?

Answer 1

D

Explanation:

reflect across the y-axis, stretch the graph vertically by a factor of 3, shift 2 units up

Answer 2

Reflect across the y-axis, stretch the graph vertically by a factor of 3, shift 2 units up.

Explanation:

The original function or the parent function is:

`f(x)=2^(x)`

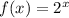
And the transformed function is:

`g(x)=3(2)^(-x)+2`

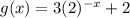
The transformations are as follows:

• Reflect the parent function about the y-axis, i.e. y : x → -x.
• Stretch the graph of the parent function vertically by 3 units, i.e.
  `3y`
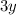
• Shift the graph, of the parent function, up by 2 units, i.e.
  `3y+2`.

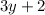The transformed function is thus:

`g(x)=3(2)^(-x)+2`.

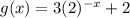Thus, the correct option is:

"Reflect across the y-axis, stretch the graph vertically by a factor of 3, shift 2 units up."