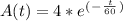Answer:
Step-by-step explanation:
Solution:-
- The amount of salt in the solution is ( A ) at any time t.
- Pure water enters the tank ( no salt ( A = 0 ) ).
- The volumetric rate of flow in and out of tank is V(flow) = 5 L / min
- The rate of change of salt in the tank at time ( t ) can be expressed as a first order ordinary differential equation for the salt solution that flows in and out of the tank
- The first order ordinary differential equation is expressed as:
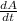 = ( salt flow in ) - ( salt flow out )
= ( salt flow in ) - ( salt flow out )
- Fresh water with zero salt content flows in then ( salt flow in ) = 0
- The concentration of salt within the tank changes with time ( t ).
- The volume of water in the tank remains constant ( steady state conditions ). I.e 5 Liters volume leaves and 5 Liters is added; hence, the total volume of solution in tank remains 300 Liters.
- So at any instant the concentration of salt in the 300 Liter tank is:
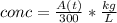
- The amount of salt-solution flowing out of the tank per unit time would be:
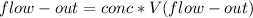
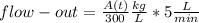
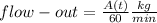
- The differential equation becomes:
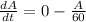
- Separate the variables and integrate both sides:

- Initial conditions: A ( 0 ) = 4 grams. Use the initial conditions to evaluate the constant of integration:
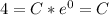
- The solution to the differential equation becomes::