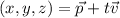The line
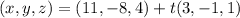
runs in the direction of its tangent vector; we can get it by taking its derivative:
![\vec T=(\mathrm d)/(\mathrm dt)\left[(11,-8,4)+t(3,-1,1)\right]=(3,-1,1)](https://img.qammunity.org/2021/formulas/mathematics/college/i0opphdkofi0lxkm5qfaiu10a7wi4sn1xs.png)
Any line that runs perpendicular to this line will have a tangent vector that is orthogonal to
 above. So construct some vector
above. So construct some vector
 that satisfies this.
that satisfies this.

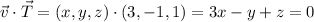
Suppose
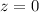 ; then
; then
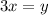 , and we can pick any two values that satisfy this condition. For instance,
, and we can pick any two values that satisfy this condition. For instance,
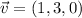
And of course,
(1, 3, 0) • (3, -1, 1) = 3 - 3 + 0 = 0
so
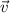 and
and
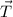 are indeed orthogonal.
are indeed orthogonal.
Now, the line running in the direction of
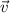 and passing through the origin can be obtained by scaling
and passing through the origin can be obtained by scaling
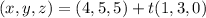
More generally, if you have a direction/tangent vector
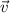 and some point
and some point
 , the line through
, the line through
 is given by
is given by