Question

According to the Rational Root Theorem, which is a factor of the polynomial f(x) = 3x3 – 5x2 – 12x + 20?

Answer 1

Explanation:

You didn't give your options, but it doesn't matter. We'll find all the possibilities and then you can pick it from your list.

When I teach this in Algebra 2, I call it the "the c over d thing" and all my students know EXACTLY to what I am referring. "c" is the constant and "d" is the leading coefficient. The combination of c/d give you the possibilities of roots for the polynomial. There are no real roots that a polynomial can have other than the possibilities we find when we do the c/d thing.

Our c is a 20. All the factors of 20 are as follows (notice that we have both the positive and negative factors):

20: ±1, ±2, ±4, ±5, ±10, ±20

Our d is a 3. All the factors of 3 are as follows (again, both the + and the -):

3: ±1, ±3 and that's it for 3.

c/d is as follows. Make sure you put ever c over every d!!!:

c/d: ±
`(1)/(1)`, ±
`(2)/(1)`, ±
`(4)/(1)`, ±
`(5)/(1)`, ±
`(10)/(1)`, ±
`(20)/(1)`, ±
`(1)/(3)`, ±
`(2)/(3)`, ±
`(4)/(3)`, ±
`(5)/(3)`, ±
`(10)/(3)`, ±
`(20)/(3)`

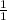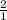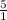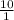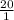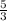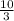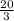
Those are all the possibilities for your roots for that polynomial. As long as the roots are real (and they won't always all be real!), there are no roots but these.

Answer 2

its D on edge

Explanation: