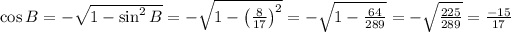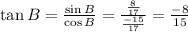Question

If sin B=8/17 WHAT IS TAN B?

Answer 1

In first quadrant,
`\tan B=(8)/(15)`

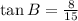
In second quadrant,
`\tan B=(-8)/(15)`

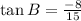
Explanation:

Given:
`\sin B=(8)/(17)`

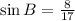
To find:
`\tan B`

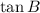
Solution:

Trigonometry explains the relationship between the sides and the angles of the triangle.

Here,

`\sin B=(8)/(17)`

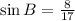
So, B can be in first or second quadrant as sine is positive both first and second quadrants.

Cosine and tangent are positive in first quadrant but negative in second quadrant.

In first quadrant:

`\cos B=√(1-\sin ^2B)=\sqrt{1-\left ( (8)/(17) \right )^2}=\sqrt{1-(64)/(289)}=\sqrt{(225)/(289)}=(15)/(17)`

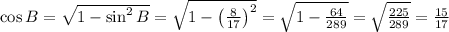
So,
`\tan B=(\sin B)/(\cos B)=((8)/(17))/((15)/(17))=(8)/(15)`

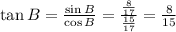
In second quadrant:

`\cos B=-√(1-\sin ^2B)=-\sqrt{1-\left ( (8)/(17) \right )^2}=-\sqrt{1-(64)/(289)}=-\sqrt{(225)/(289)}=(-15)/(17)`

`\tan B=(\sin B)/(\cos B)=((8)/(17))/((-15)/(17))=(-8)/(15)`