Question

An observer (0) spots a plane flying at a 55° angle to his horizontal line of sight. If the plane is flying at an altitude of 21,000 ft., what is the distance (x)

from the plane (P) to the observer (O)? (4 points)
A)20,793 ft
B)28,793 ft
C)36,585 ft
D)25,636 ft

Answer 1

Option D. 25636 ft

Answer 2

Option D. 25636 ft

Explanation:

From the given right triangle,

Observer is at the point O and he observes the plane flying at point P.

Angel of elevation of the plane is 55° and altitude of the plane was 21000 ft.

To get the distance OP we will apply Sine rule in the given right triangle,

Sin 55 =
`(h)/(x)`

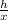
Sin 55 =
`(21000)/(x)`

x =
`\frac{21000}{\text{sin}55}`

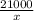
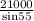
x = 25636.27

x ≈ 25636 ft

Therefore, distance between the plane and observer is 25636 ft.

Option D. is the answer