Question

Consider the initial value problem y′+2y=4t,y(0)=8.

a. Take the Laplace transform of both sides of the given differential equation to create the corresponding algebraic equation. Denote the Laplace transform of y(t) by Y(s).
b. Solve your equation for Y(s).
c. Take the inverse Laplace transform of both sides of the previous equation to solve for y(t).

Answer 1

Please read the complete procedure below:

Explanation:

You have the following initial value problem:

`y'+2y=4t\\\\y(0)=8`

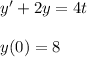
a) The algebraic equation obtain by using the Laplace transform is:

`L[y']+2L[y]=4L[t]\\\\L[y']=sY(s)-y(0)\ \ \ \ (1)\\\\L[t]=(1)/(s^2)\ \ \ \ \ (2)\\\\`

next, you replace (1) and (2):

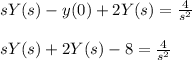`sY(s)-y(0)+2Y(s)=(4)/(s^2)\\\\sY(s)+2Y(s)-8=(4)/(s^2)` (this is the algebraic equation)

b)

`sY(s)+2Y(s)-8=(4)/(s^2)\\\\Y(s)[s+2]=(4)/(s^2)+8\\\\Y(s)=(4+8s^2)/(s^2(s+2))` (this is the solution for Y(s))

c)

`y(t)=L^(-1)Y(s)=L^(-1)[(4)/(s^2(s+2))+(8)/(s+2)]\\\\=L^(-1)[(4)/(s^2(s+2))]+L^(-1)[(8)/(s+2)]\\\\=L^(-1)[(4)/(s^2(s+2))]+8e^(-2t)`

To find the inverse Laplace transform of the first term you use partial fractions:

`(4)/(s^2(s+2))=(-s+2)/(s^2)+(1)/(s+2)\\\\=((-1)/(s)+(2)/(s^2))+(1)/(s+2)`

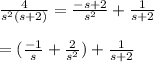
Thus, you have:

`y(t)=L^(-1)[(4)/(s^2(s+2))]+8e^(-2t)\\\\y(t)=L^(-1)[(-1)/(s)+(2)/(s^2)]+L^(-1)[(1)/(s+2)]+8e^(-2t)\\\\y(t)=-1+2t+e^(-2t)+8e^(-2t)=-1+2t+9e^(-2t)`

(this is the solution to the differential equation)