Question

In a study of cell phone usage and brain hemispheric​ dominance, an Internet survey was​ e-mailed to 6967 subjects randomly selected from an online group involved with ears. There were 1331 surveys returned. Use a 0.01 significance level to test the claim that the return rate is less than​ 20%. Use the​ P-value method and use the normal distribution as an approximation to the binomial distribution.

Answer 1

`z=\frac{0.191 -0.2}{\sqrt{(0.2(1-0.2))/(6967)}}=-1.878`

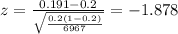
Now we can find the p value using the alternative hypothesis and with the following probability:

`p_v =P(z<-1.878)=0.0302`

We see that the p value is higher than the significance level of 0.01 so then we FAIL to reject the null hypothesis and there is NOT enough evidence to conclude that the return rate is less than​ 20% at 1% of significance

Explanation:

Information given

n=6967 represent the random sample selected

X=1331 represent the surveys returned

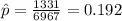`\hat p=(1331)/(6967)=0.192` estimated proportion of return rate

tex]p_o=0.2[/tex] is the value to verify

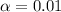`\alpha=0.01` represent the significance level

z would represent the statistic

`p_v` represent the p value

System of hypothesis

We test the claim that the return rate is less than​ 20%, then the system of hypothesis are:

Null hypothesis:
`p\geq 0.2`

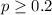
Alternative hypothesis:
`p < 0.2`

The statistic is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

Replacing the info given we got:

`z=\frac{0.191 -0.2}{\sqrt{(0.2(1-0.2))/(6967)}}=-1.878`

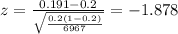
Now we can find the p value using the alternative hypothesis and with the following probability:

`p_v =P(z<-1.878)=0.0302`

We see that the p value is higher than the significance level of 0.01 so then we FAIL to reject the null hypothesis and there is NOT enough evidence to conclude that the return rate is less than​ 20% at 1% of significance