Answer:
a) Cancellations are independent and similar to arrivals.
b) 22.31% probability that no cancellations will occur on a particular Wednesday
Explanation:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

In which
x is the number of sucesses
e = 2.71828 is the Euler number
 is the mean in the given time interval.
is the mean in the given time interval.
Mean rate of 1.5 per day on a typical Wednesday.
This means that
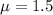
(a) Justify the use of the Poisson model.
Each wednesday is independent of each other, and each wednesday has the same mean number of cancellations.
So the answer is:
Cancellations are independent and similar to arrivals.
(b) What is the probability that no cancellations will occur on a particular Wednesday
This is P(X = 0).

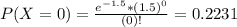
22.31% probability that no cancellations will occur on a particular Wednesday