We have been given an expression
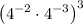 . We have been given steps how Chris tried to solve the given expression. We are asked to choose the correct option about Chris's work.
. We have been given steps how Chris tried to solve the given expression. We are asked to choose the correct option about Chris's work.
Let us simplify our given expression.
Using exponent property,
 , we cab rewrite our given expression as:
, we cab rewrite our given expression as:

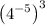
Now we will use exponent property
 to further simplify our expression.
to further simplify our expression.
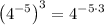
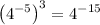
Therefore, Chris made mistake in step 2.