Which is the equation of a hyperbola centered at the origin with vertex (2, 0) that passes through 4,3 )?

Question

asked Jun 26, 2021 83.2k views

2 Answers

Bboydflo · Answer 1 · 2021-07-03T19:05:03+0000

Answer:

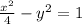(x^(2))/(4) - y^(2) = 1 (Option B)

Explanation:

The hyperbola has the following vertices:
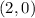(2,0) and
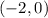(-2,0) . The first constant of the hyperbola is:

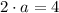
$2\cdot a = 4$

a = 2

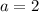
The other constant is determined by using the standard equation of the hyperbola and replacing all known variables:

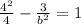
(4^(2))/(4) - (3)/(b^(2)) = 1

4 - (3)/(b^(2)) = 1

(3)/(b^(2)) = 3

b^(2) = 1

b = 1

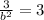
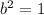
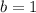
The equation of the hyperbola in standard form is:

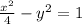(x^(2))/(4) - y^(2) = 1 (Option B)