Question

You have been hired by a company which is designing a new water slide for an amusement park. The conceptual design has a customer going down a curved slide ending up moving horizontally at the bottom. At the end of the slide, the customer grabs the end of a 16.0 m long vertical bar that is free to pivot about its center. After grabbing onto the bar, the customer swings out over a pool of water. When the bar swings out to its maximum distance, the customer can drop off and fall straight down into the water.

1. Your task is to determine the height of the slide so that the maximum horizontal distance that the bar swings out is 5.0 m for a 60 kg person. The bar has five times the mass of a 60 kg person. From an engineering handbook, you find that the moment of inertia of the bar is 1/12 of what it would be if all of its mass were concentrated at the bottom.

Answer 1

the height of the slide is 4.68 m

Step-by-step explanation:

The top of side to bottom of side is shown by the expression:

`mgh = (1)/(2) mv_or`

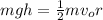
where ;

`v_o =√(2gh)`

Using Conservation of angular momentum after collision with the vertical bar; we have:

`I_1 \omega_1 + I_2 \omega_2 = I \omega`

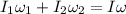
where ;

`\omega_2 =0`

Then:

`I _1 \omega_1 = I \omega`

`mR^2((v_o)/(R) ) = (mR^2+ (1)/(12)5 mL^2) (v_1)/(R)`

`mRv_o = (mR^2+ (5)/(12) m(2R)^2)(v_1)/(R)`

`R√(2gh) = (R+(10)/(6)r)v_1`

`√(2gh ) = (16)/(6) v_1`

`√(2gh ) = (8)/(3) v_1`

`v_1 = (3)/(8) √(2gh)`

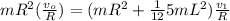
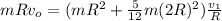
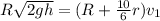
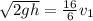
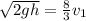
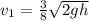
Using the approach from conservation of energy for The linear speed of the person after grabbing bar; we have:

`(1)/(2)I \omega^2 = mgh_2`

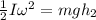
where
`\omega = (v_1)/(R) , R = (16)/(2) =8 \ m`

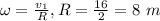
Then;

`(1)/(2) (mR^2+(5)/(12) m(2R)^2)(v_1^2)/(R^2) = mgh_2`

`(1)/(2) (R^2+(20)/(12) R^2)(v_1^2)/(R^2) = gh_2`

`(1)/(2) ((32)/(12)){v_1^2}= gh_2`

`((32)/(24)){v_1^2}= gh_2`

`\frac{4}3((9)/(64)2gh) = gh_2 \\ \\ (3)/(8)h = h_2 \\ \\ h = (8)/(3)h_2`

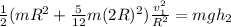
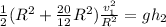
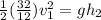
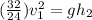
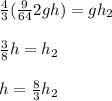
where;

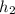`h_2` = 1.775 m

i.e The final height of the end of the bar and the rider will rise up as the bar swings out to 5.0 m if you make a triangle with the hypotenuse 8.0 m and the bottom 5.0m and then subtract the third side from 8.0 m you get the difference in height from the bar being directly vertical vs the height reached during the swing.
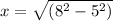`x =√((8^2-5^2))` = 6.245

8.0 m - x = 8.0 m - 6.245 = 1.755 m which is the final height
`h_2`

`h = (8)/(3)h_2`

`h = (8)/(3)*1.755\ m`

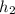
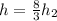
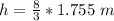
h = 4.68 m

Hence, the height of the slide is 4.68 m