Question

The manufacturers of a deodorant claim that the mean drying time of their product is, at most, 15 minutes. A sample consisting of 16 cans of the product was used to test the manufacturer's claim. The experiment yielded a mean drying time of 18 minutes with a standard deviation of 6 minutes. Find the t-test and the p-value, and state your conclusion at the 5% significance level.

O t = 2, 2.5% < p-value < 5%, reject the null hypothesis. There enough evidence to conclude that the mean drying time is greater than 15 minutes.
O t = 2, 2.5% < p-value < 5%, fail to reject the null hypothesis. There is not enough evidence to conclude that the mean drying time is greater than 15 minutes.
O t = 2, p-value > 5%, reject the null hypothesis. There enough evidence to conclude that the mean drying time is greater than 15 minutes.
O t = 2, p-value > 5%, fail to reject the null hypothesis. There is not enough evidence to conclude that the mean drying time is greater than 15 minutes.

Answer 1

`t = (18-15)/((6)/(√(16)))= 2`

`df = n-1= 16-1=15`

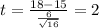
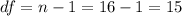
And the p value since we have a right tailed test is given by:

`p_v= P(t_(15)>2) = 0.0639`

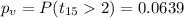
And for this case the p value is higher than the significance level of 0.05 so then we have enough evidence to FAIL to reject the null hypothesis and the best conclusion for this case is:

t = 2, p-value > 5%, fail to reject the null hypothesis. There is not enough evidence to conclude that the mean drying time is greater than 15 minutes.

Explanation:

For this problem we have the following info given:

`n = 16` represent the sample size

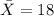`\bar X = 18` represent the sample mean for the drying time

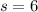`s= 6` represent the sample deviation

We want to test the claim that the mean drying time of their product is, at most, 15 minutes, so then the system of hypothesis are:

Null hypothesis:
`\mu \leq 15`

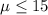
Alternative hypothesis:
`\mu >15`

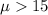
The statistic is given by this formula since we don't know the population deviation:

`t = (\bar X -\mu)/((s)/(√(n)))`

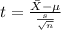
And replacing we have:

`t = (18-15)/((6)/(√(16)))= 2`

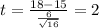
Now we can find the degrees of freedom given by:

`df = n-1= 16-1=15`

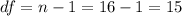
And the p value since we have a right tailed test is given by:

`p_v= P(t_(15)>2) = 0.0639`

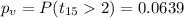
And for this case the p value is higher than the significance level of 0.05 so then we have enough evidence to FAIL to reject the null hypothesis and the best conclusion for this case is:

t = 2, p-value > 5%, fail to reject the null hypothesis. There is not enough evidence to conclude that the mean drying time is greater than 15 minutes.