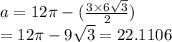Answer:
The area is roughly 22.1106cm².
Explanation:
The area of the entire circle would be:

However, we only have 120° of it, which out of 360° means we have 1/3 of the circle, and therefore the sector is:
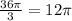
Using the Law of Cosines, it is possible to find the missing side of the triangle:
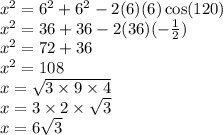
Then, to calculate the area of the triangle, we find its height using the Pythagorean Theorem.
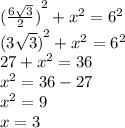
Finally, we calculate the area of the triangle and subtract it from the sector.