Question

A machine is used to fill Apple Juice bottles with juice. The machine has a known standard deviation of σ = 0.05 liters. The target mean fill volume is µ = 2.0 liters. A quality control manager obtains a random sample of 50 bottles. He will shut down the machine if the sample of these 50 bottles is less than 1.95 or greater than 2.1. What is the probability that the quality control manager will shut down the machine?

Answer 1

The probability that the quality control manager will shut down the machine is 0.0002.

Explanation:

We are given that a machine is used to fill Apple Juice bottles with juice. The machine has a known standard deviation of σ = 0.05 liters. The target mean fill volume is µ = 2.0 liters.

A quality control manager obtains a random sample of 50 bottles. He will shut down the machine if the sample of these 50 bottles is less than 1.95 or greater than 2.1.

Let
`\bar X` = sample mean fill volume

The z score probability distribution for sample mean is given by;

Z =
`(\bar X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\mu` = population mean fill volume = 2 liters

`\sigma` = standard deviation = 0.05 liters

n = sample of bottles = 50

Now, it is provided that he will shut down the machine if the sample of these 50 bottles is less than 1.95 or greater than 2.1.

• So, Probability that the sample of these 50 bottles is less than 1.95 is given by = P(
  `\bar X` < 1.95)

P(
`\bar X` < 1.95) = P(
`(\bar X-\mu)/((\sigma)/(√(n) ) )` <
`(1.95-2)/((0.05)/(√(50) ) )` ) = P(Z < -7.07) = 1 - P(Z
`\leq` 7.07)

= 1 - 0.9999 = 0.0001

• Probability that the sample of these 50 bottles is greater than 2.1 is given by = P(
  `\bar X` > 2.1)

P(
`\bar X` > 2.1) = P(
`(\bar X-\mu)/((\sigma)/(√(n) ) )` >
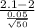`(2.1-2)/((0.05)/(√(50) ) )` ) = P(Z > 14.14) = 1 - P(Z < 14.14)

= 1 - 0.9999 = 0.0001

Because the highest critical value in the z table is given as x = 4.40 for area of 0.99999.

Therefore, probability that the quality control manager will shut down the machine = 2
`*` 0.0001 = 0.0002.