Answer:
33.6
Explanation:
As we can see in the graph, the points:
- P is located at (-2, 8)
- Q is located at ( 6, 8)
- R( is located at (6, 2)
- S is located at (-5, 0)
To find a distance between two points or the length of the segment, we use the following formula:
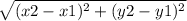
Because the two points P and Q are located at the same libe y = 8
=> the lenght of PQ =

Because the two points R and Q are located at the same libe x = 6
=> the length of RQ =
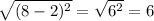
The lenght of RS is:
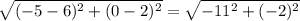 =
=
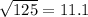
The lenght of SP is:
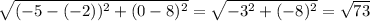 = 8.5
= 8.5
=> the perimeter of quadrilateral PQRS = PQ+RQ+RS+SP
= 8+6+11.1+8.5
= 33.6