Question

Suppose the S&R index is 800, the continuously compounded risk-free rate is 5%, and the dividend yield is 0%. A 1-year 815-strike European call costs $75 and a 1- year 815-strike European put costs $45. Consider the strategy of buying the stock, selling the 815-strike call, and buying the 815-strike put. a. What is the rate of return on this position held until the expiration of the options? b. What is the arbitrage implied by your answer to (a)? c. What difference between the call and put prices would eliminate arbitrage? d. What difference between the call and put prices eliminates arbitrage for strike prices of $780, $800, $820, and $840?

Answer 1

a) the rate of return on this position held until the expiration of the options is r = 0.05638

b) $5.52

c) C - P = $24.748

d)

• C - P = $4.748
• C - P = $24.748
• C - P = $44.748
• C - P = $64.748

Step-by-step explanation:

a) Assume that, we are buying the stock, selling the 815-strike call , and buying the 815 strike put, the rate of return on this position held until the expiration of the options can be determined as follows:

solving for the cost first; we have:

(- $800 + $75 - $45) = $770

After 1-year ; the compounded rate of return (r) can be expressed as:

`770e^r = 815`

`e^r = (815)/(770) \\ \\ e^r = 1.058 \\ \\ e = In(1.058) \\ \\ r = 0.05638`

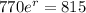
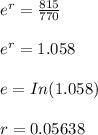
Thus, the rate of return on this position held until the expiration of the options is r = 0.0564

b)

What is the arbitrage implied by your answer to (a)?

The return rate on this position shows more interest than the risk-free interest rate. However, there is need to borrow money at 5% (0.05) in order to purchase a large amount of the rate of return position of (a), resulting into a sure return of 0.64%. In essence, $770 is being borrowed from the bank to buy and secure one position; Therefore , after 1-year; the bank is being owed:

$
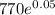`770e^(0.05)` = $809.48

Thus, the arbitrage implied by the answer to (a) is:

$815 - $809.48 = $5.52

c) . What difference between the call and put prices would eliminate arbitrage? To eliminate arbitrage; it is crucial that the call and put prices should be on hold. This implies that:

C - P =
`S_o - Ke^(-rT)`

C - P =
`800 - 815 e^(-rT)`

C - P =
`800 - 815 e^(-0.05*1)`

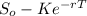
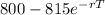
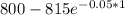
C - P = $24.748

d). What difference between the call and put prices eliminates arbitrage for strike prices of $780, $800, $820, and $840?

C - P =
`S_p - Ke^(-rT)`

where
`S_p` is the spike prices

when
`S_p` = $780

C - P =
`780 - 815 e ^{-0.05*1`

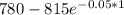
C - P = $4.748

when
`S_p` = $800

C - P =
`800 - 815 e^(-0.05*1)`

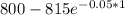
C - P = $24.748

when
`S_p` = $820

C - P =
`820 - 815 e^(-0.05*1)`

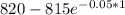
C - P = $44.748

when
`S_p` = $840

C - P =
`840 - 815 e^(-0.05*1)`

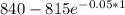
C - P = $64.748