Question

Football teams toss a coin to see who will get their choice of kicking or receiving to begin a game. Also, if the game goes into overtime, they must do another coin toss to determine who will kick or receive at the beginning of the overtime period. Suppose the coin is not fair, and has a probability of .3 of showing up heads. If a team always guesses heads, what is the probability that they WON'T win both coin tosses? (Assuming that the game does in fact go into overtime)a.09b.91c.49d.51

Answer 1

`P(H) = 0.3`

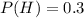
And the probability of tails
`P(T) = 1-0.3 =0.7`

The probability of win in both tosses assuming the condition given that the game in fact go to overtime and that the events are independnet would be:

`P(H \cap H) = P(H) *P(H)`

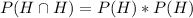
And replacing we got

`P(H \cap H) = 0.3 *0.3=0.09`

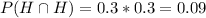
And then the probability of not win in both games by the complement rule is

`1-0.09 =0.91`

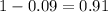
So the best answer would be:

b.91

Explanation:

For this case we know that the team always select the option heads for the game and for overtime, and we know that the coin is biased with the probability of heads given by:

`P(H) = 0.3`

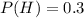
And the probability of tails
`P(T) = 1-0.3 =0.7`

The probability of win in both tosses assuming the condition given that the game in fact go to overtime and that the events are independnet would be:

`P(H \cap H) = P(H) *P(H)`

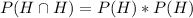
And replacing we got

`P(H \cap H) = 0.3 *0.3=0.09`

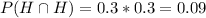
And then the probability of not win in both games by the complement rule is

`1-0.09 =0.91`

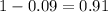
So the best answer would be:

b.91