At Sanger’s auto garage, three out of every five cars brought in for service need an oil change. Of the cars that need an oil change, four out of every seven also need a tire ro…

Question

asked Nov 14, 2021 213k views

2 Answers

Astoria · Answer 1 · 2021-11-20T13:05:37+0000

Answer:

The probability that a car that comes into the garage needs both an oil change and a tire rotation is
(12)/(35) .

Explanation:

The conditional probability of an event B given that another event A has already occurred is:

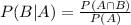
$P(B|A)=(P(A\cap B))/(P(A))$

Denote the events as follows:

X = cars brought in for service need an oil change

Y = cars brought in for service need a tire rotation

The information provided is:

P(X)=(3)/(5)

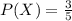
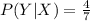
P(Y|X)=(4)/(7)

Compute the value of P (X ∩ Y) as follows:

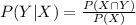
$P(Y|X)=(P(X\cap Y))/(P(X))$

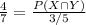
$(4)/(7)=(P(X\cap Y))/(3/5)$

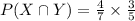
$P(X\cap Y)=(4)/(7)* (3)/(5)$

=(12)/(35)

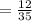
Thus, the probability that a car that comes into the garage needs both an oil change and a tire rotation is
(12)/(35) .