Given:
Given that the sum of the areas of two rectangles is 212 m². The second rectangle is 12 m² smaller than three times the first rectangle.
We need to determine the areas of the two rectangles.
Equations of the two rectangles:
Let a₁ denote the area of the first rectangle.
Let a₂ denote the area of the second rectangle.
The equations of the two rectangles is given by
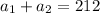 and
and
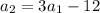
Areas of the two rectangles:
The areas of the two rectangles can be determined using substitution method.
Thus, substituting
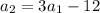 in the equation
in the equation
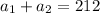 , we get;
, we get;

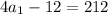

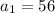
Thus, the area of the first rectangle is 56 m²
Substituting
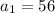 in the equation
in the equation
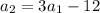 , we get;
, we get;


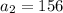
Thus, the area of the second rectangle is 156 m²
Hence, the area of the two rectangles are 56 m² and 156 m²