Question

Bastien, Inc. has been manufacturing small automobiles that have averaged 50 miles per gallon of gasoline in highway driving. The company has developed a more efficient engine for its small cars and now advertises that its new small cars average more than 50 miles per gallon in highway driving. An independent testing service road-tested 36 of the automobiles. The sample showed an average of 51.5 miles per gallon. The population standard deviation is 6 miles per gallon. You conduct a test with a 0.05 level of significance to determine whether or not the manufacturer's advertising campaign is legitimate. What is the p-value associated with the sample results (2 decimals)?

Answer 1

To evaluate the manufacturer's claim, we can use a one-sample t-test. The test statistic is calculated as t = 1.5 and the p-value is 0.0758. Since the p-value is greater than 0.05, we fail to reject the null hypothesis.

Step-by-step explanation:

To conduct a hypothesis test to evaluate the manufacturer's claim, we can use a one-sample t-test. The null hypothesis (H0) is that the true population mean is equal to 50 miles per gallon, while the alternative hypothesis (Ha) is that the true population mean is greater than 50 miles per gallon. The significance level (alpha) is 0.05.

First, we calculate the test statistic using the formula:

t = (sample mean - population mean) / (population standard deviation / sqrt(sample size))

Substituting the given values, we get:

t = (51.5 - 50) / (6 / sqrt(36))

Simplifying this equation gives:

t = 1.5 / (6 / 6)

t = 1.5

Next, we calculate the p-value associated with this test statistic using a t-distribution table or a statistical software. In this case, the p-value is 0.0758 (rounded to 4 decimal places), which is greater than the significance level of 0.05.

Since the p-value is greater than the significance level, we fail to reject the null hypothesis. This means that there is not enough evidence to support the manufacturer's claim that the new small cars average more than 50 miles per gallon in highway driving.

Answer 2

We conclude that the the manufacturer's advertising campaign is not correct.

P-value of test = 0.067.

Step-by-step explanation:

We are given that an independent testing service road-tested 36 of the automobiles. The sample showed an average of 51.5 miles per gallon. The population standard deviation is 6 miles per gallon.

We have to conduct a test to determine whether or not the manufacturer's advertising campaign is legitimate.

Let
`\mu` = population average gasoline of new small cars in highway driving.

SO, Null Hypothesis,
`H_0` :
`\mu`
`\leq` 50 miles per gallon {means that the manufacturer's advertising campaign is not correct}

Alternate Hypothesis,
`H_A` :
`\mu` > 50 miles per gallon {means that the manufacturer's advertising campaign is correct}

The test statistics that will be used here is One-sample z test statistics as we know about the population standard deviation;

T.S. =
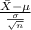`(\bar X -\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\bar X` = sample average gasoline = 51.5 miles per gallon

`\sigma` = population standard deviation = 6 miles per gallon

n = sample of automobiles = 36

So, test statistics =
`(51.5-50)/((6)/(√(36) ) )`

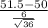
= 1.50

Now at 0.05 significance level, the z table gives critical value of 1.6449 for right-tailed test. Since our test statistics is less than the critical values of z as 1.50 < 1.6449, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region.

Also, P-value is given by the following formula;

P-value = P(Z > 1.50) = 1 - P(Z
`\leq` 1.50)

= 1 - 0.93319 = 0.067 or 6.7%

Therefore, we conclude that the the manufacturer's advertising campaign is not correct as its new small cars average less than or equal to 50 miles per gallon in highway driving.