Question

Oil (SAE 30) at 15.6 oC flows steadily between fixed, horizontal, parallel plates. The pressure drop per unit length along the channel is 40 kPa/m, and the distance between the plates is 4 mm. The flow is laminar. Determine: (a) the volume rate of flow (per meter of width), (b) the magnitude of the shearing stress acting on the bottom plate, and (c) the velocity along the centerline of the channel.

Answer 1

a) Volume rate of flow = 0.00056 m³/s

b) Shearing stress acting at the bottom = 80 N/m²

c) Velocity along the center line of the channel = 0.211 m/s

Step-by-step explanation:

Pressure drop per unit length,
`(dP)/(dl) = 40 kPa/m`

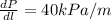
dp = 40 kPa

The distance between the plates, l = 4 mm = 0.004 m

Distance between the horizontal plate and the center, h = 0.004/2 = 0.002 m

`\mu = 0.38 Ns/m^(2)`

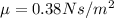
a) The volume rate of flow,
`v = (2h^(3) )/(3 \mu)* (\delta p)/(\delta l)`

`v = (2* 0.002^(3) * 40 * 10^(3) )/(3*0.38)`

`v = 0.00056 m^(3) /s`

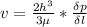
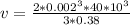
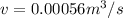
b) The magnitude of the shearing stress acting at the bottom

Shear stress,
`\tau = h dP`

`\tau = 0.002 * 40000\\\tau = 80 N/m^(2)`

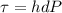
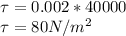
c) The velocity along the center line of the channel

velocity, v =
`(h^(2) )/(2 \mu) * (\delta p)/(\delta l)`

v =
`(0.002^(2) )/(2 * 0.38) * 40000`

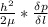
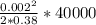
v = 0.211 m/s