Question

A rectangular box is going to be made with a volume of 274 cm3. The base of the box will be a square and the top will be open. The cost of the material for the base is 0.3 cents per square centimeter, and the cost of the material for the sides is 0.1 cents per square centimeter. Determine the dimensions of the box that will minimize the cost of manufacturing it. What is the minimum cost?

Answer 1

0.29

Explanation:

Answer 2

The dimensions of the box are 5.67 cm by 5.67 cm by 8.51 cm.

The total minimum cost = 28.97 cents.

Explanation:

Let the base dimensions are a cm by a cm and the height is h cm.

So, a²h = 274 ............. (1)

And, total cost, C = 0.3a² + 0.1 × 4ah = 0.3a² + 0.4ah

C = 0.3a² + 0.4 × (274/a) ................. (2)

Now, for minimum total cost, the condition is
`(dC)/(da) = 0 = 0.6a - (0.4 * 274)/(a^(2) )`

⇒
`a^(3) = (0.4 * 274)/(0.6) = 182.67`

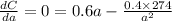
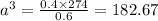
⇒ a = 5.67 cm

So,
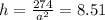`h = (274)/(a^(2)) = 8.51` cm.

Therefore, the dimensions of the box are 5.67 cm by 5.67 cm by 8.51 cm.

And the total minimum cost =
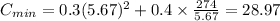`C_(min) = 0.3 (5.67)^(2) + 0.4 * (274)/(5.67) = 28.97` cents. (Answer)