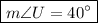Question

Given ΔSTU and ΔDEF, what is m∠U ?

Answer 1

In this context:

`\boxed{m\angle U=40^(\circ)}`

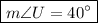
Step-by-step explanation:

Hello! Remember you have to write complete questions in order to get good and exact answers. Here you haven't provided any diagram, so I'll assume ΔSTU and ΔDEF are similar. Two triangles are similar if and only if their corresponding angles are congruent and their corresponding sides are in proportion.

So:

`\angle S=\angle D \ldots eq1 \\ \\ \angle T=\angle E \ldots eq2 \\ \\ \angle U=\angle F \ldots eq3`

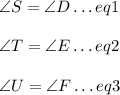
We also know:

`\angle S+\angle T+\angle U=180^(\circ) \ldots eq4 \\ \\ \angle D+\angle E+\angle F=180^(\circ) \ldots eq5`

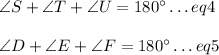
Suppose we know:

`\angle S=30^(\circ) \\ \\ \angle E=110^(\circ)`

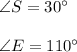
Then, by eq2:

`\angle T=\angle E =110^(\circ)`

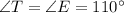
By substituting ∠S and ∠T into eq4:

`\angle S+\angle T+\angle U=180^(\circ) \\ \\ 30^(\circ)+110^(\circ)+\angle U=180^(\circ) \\ \\ \\ Isolating \ \angle U: \\ \\ \angle U=180^(\circ)-(30^(\circ)+110^(\circ)) \\ \\ \angle U=180^(\circ)-140^(\circ) \\ \\ \angle U=40^(\circ)`

Finally:

`\boxed{m\angle U=40^(\circ)}`