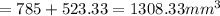Answer:
Explanation:
The volume of the composite shape is given by:
Volume of cylinder +volume of two spheres.
The volume of cylinder
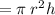
We substitute r=5mm and h=10mm
The volume cylinder becomes
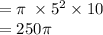

The volume of the two hemispheres
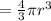
We substitute the radius to get:

We add the two volumes to get: