Question

Gabrielle is cutting a triangular sign with a base of 8 inches. The perpendicular distance from the base of the sign to its vertex is 9 inches. What is the area of the sign?

Answer 1

36 in squared

Explanation:

Answer 2

The area of the triangular sign is 36 square inches, if Gabrielle is cutting a triangular sign with a base of 8 inches and the perpendicular distance from the base of the sign to its vertex is 9 inches.

Explanation:

The given is,

Gabrielle is cutting a triangular sign

Base of 8 inches

The perpendicular distance from the base of the sign to its vertex is 9 inches

Step:1

Formula for area of triangle is,

Area,
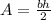`A = (bh)/(2)`.....................................(1)

Where, b - Base of triangle

h - Height of triangle

From given value,

b - 8 inches

h - 9

Equation (1) becomes,

`A = ((8)(9))/(2)`

`=(72)/(2)`

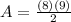
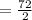
= 36

Area of triangle sign, A = 36 square inches

Result:

The area of the triangular sign is 36 square inches, if Gabrielle is cutting a triangular sign with a base of 8 inches and the perpendicular distance from the base of the sign to its vertex is 9 inches.