Answer:
63% of the values lies between 70 and 85.
Explanation:
We are given that a normally distributed set of numbers has a mean of 75 and a standard deviation of 7.97.
Let X = Set of numbers
The z-score probability distribution for is given by;
Z =
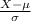 ~ N(0,1)
~ N(0,1)
where,
 = mean value = 75
= mean value = 75
 = standard deviation = 7.97
= standard deviation = 7.97
The Z-score measures how many standard deviations the measure is away from the mean. After finding the Z-score, we look at the z-score table and find the p-value (area) associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X.
So, percentage of values that lies between 70 and 85 is given by = P(70 < X < 85) = P(X < 85) - P(X
 70)
70)
P(X < 85) = P(
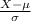 <
<
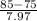 ) = P(Z < 1.25) = 0.89435 {using z table}
) = P(Z < 1.25) = 0.89435 {using z table}
P(X
 70) = P(
70) = P(
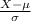

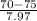 ) = P(Z
) = P(Z
 -0.63) = 1 - P(Z < 0.63)
-0.63) = 1 - P(Z < 0.63)
= 1 - 0.73565 = 0.26435
Now, in the z table the P(Z
 x) or P(Z < x) is given. So, the above probability is calculated by looking at the value of x = 1.25 and x = 0.63 in the z table which has an area of 0.89435 and 0.73565 respectively.
x) or P(Z < x) is given. So, the above probability is calculated by looking at the value of x = 1.25 and x = 0.63 in the z table which has an area of 0.89435 and 0.73565 respectively.
Therefore, P(70 < X < 85) = 0.89435 - 0.26435 = 0.63 or 63%
Hence, 63% of the values lies between 70 and 85.