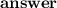
➡️The sequence has a common difference of 4, so is an arithmetic sequence. The formula for the n-th term of an arithmetic sequence is .
an = a1 + d(n -1)
where a1 is the first term (-17) and d is the common difference (4).
Then the 75th term is ...
a75 = -17 + 4(75 -1) = -17 +296 = 279
The 75th term is 279.