Question

a researcher wishes to estimate the mean number of miles driven by 4-year-old cars. The population standard deviation of miles driven by all chevy owners is 15,500 milesl how man cars must be sampled so that a 92% confidence interval will have a margin of error of 1000 miles?

Answer 1

The sample size must be approximately 1304.

Explanation:

We are given the following in the question:

Population standard deviation = 15,500 miles

We have to construct a 92% confidence interval with margin of error of 1000 miles.

Margin of error =

`z_(critical)* (\sigma)/(√(n))`

`z_(critical)\text{ at}~\alpha_(0.02) = \pm 2.33`

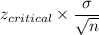
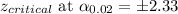
Putting values, we get,

`2.33* (15500)/(√(n)) = 1000\\\\√(n) = 2.33* (15500)/(1000) \\√(n) = 36.115\\n = 1304.29\\n\approx 1304`

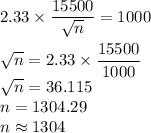
The sample size must be approximately 1304.