Answer:
b)the angular speed after 3.6s is is 12.7rad/s
c) the angular acceleration of the reel is 3.52rad/s²
Step-by-step explanation:
b)
The angle in radian is represented as follows
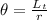
r = 16.2cm = 0.162m
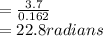
now,
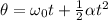
where
 is the angular speed
is the angular speed
 is the angular acceleration
is the angular acceleration
t is the time

the first equation of motion is represeented by
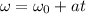

the angular speed after 3.6s is is 12.7rad/s
c)
from the above calculation , angular acceleration is calculated as
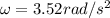
Therefore, the angular acceleration of the reel is 3.52rad/s²