Question

A function that represents the exponential function f(x)= 3 to the power of x after a vertical stretch by a factor of 8 and a reflection across the x-axis

Answer 1

A function that represents the exponential function f(x)= 3 to the power of x after a vertical stretch by a factor of 8 and a reflection across the x-axis is
`f(x) = -8(3^x)` .

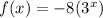Explanation:

Here we have to make A function that represents the exponential function f(x)= 3 to the power of x after a vertical stretch by a factor of 8 and a reflection across the x-axis . Let's find out:

We have ,

• A function that represents the exponential function f(x)= 3 to the power of x

Following is the equation for above statement :

⇒
`f(x) = 3^x`

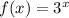
• A vertical stretch by a factor of 8

Following is the equation for above statement :

⇒
`f(x) = 8(3^x)`

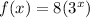
• A reflection across the x-axis

Following is the equation for above statement :

⇒
`f(x) = 8(3^x)(-1)`

⇒
`f(x) = -8(3^x)`

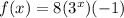
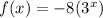
Therefore , A function that represents the exponential function f(x)= 3 to the power of x after a vertical stretch by a factor of 8 and a reflection across the x-axis is
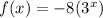`f(x) = -8(3^x)` .