Question

You want to estimate the proportion of students at your college or university who are employed for 10 or more hours per week while classes are in session.

You plan to present your results by a 95% confidence interval. Using the guessed value p* = 0.34, find the sample size required if the interval is to have an approximate margin of error of m = 0.07.

Answer 1

The minimum sample size required to estimate the required proportion is 176 students.

Explanation:

We are given the following data:

Guessed sample proportion = p = 0.34

Margin of Error = m = 0.07

Confidence Interval = 95%

We need to calculate the minimum sample size required. Since we are dealing with proportions, we will use the formulas of one-sample z-test for population proportions, according to which:

`m=z * \sqrt{(p(1-p))/(n) }`

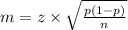
The value of z can be seen from the z-tables or z-calculators. The z value for 95% confidence interval comes out to be 1.96

Substituting the values in the above formula gives us:

`0.07=1.96 * \sqrt{(0.34(1-034))/(n) } \\\\ 0.07=1.96 * (√(0.34(0.66)))/(√(n))\\\\√(n) =(1.96)/(0.07) * √(0.34 * 0.66)\\\\ n=((1.96)/(0.07))^(2) * 0.34 * 0.66\\\\ n=175.93`

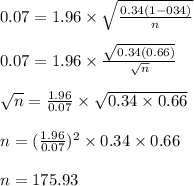
Thus, the minimum sample size required to estimate the required proportion is 176 students.