The solution to the system of equations is
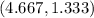
Step-by-step explanation:
Given that the two equations are
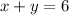 and
and
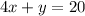
We need to determine the solution of the system of equations graphically.
Let us consider the equation
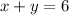
We shall plot the equation
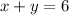 in the graph using the x and y intercepts.
in the graph using the x and y intercepts.
Substituting
 , we get,
, we get,
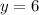
Substituting
 , we get,
, we get,
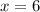
Thus, the x and y intercepts of the equation
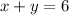 are
are
 and
and
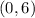 respectively.
respectively.
Hence, joining these two coordinates, we get, the line for the equation
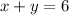
Now, we shall consider the equation
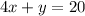
We shall plot the equation
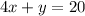 in the graph using the x and y intercepts.
in the graph using the x and y intercepts.
Substituting
 , we get,
, we get,
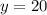
Substituting
 , we get,
, we get,

Thus, the x and y intercepts of the equation
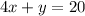 are
are
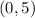 and
and
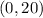 respectively.
respectively.
Hence, joining these two coordinates, we get, the line for the equation
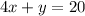
The solution to the system of equations is the point of intersection of these two lines.
Hence, the point of intersection of these two lines is
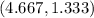
Therefore, the solution to the system of equations is
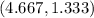
The image of the graph containing the solution is attached below: