The number of miles driven by a truck driver in a day falls between 200 and 500, and follows a uniform distribution. (a) Find the probability that the truck driver goes more tha…

Question

asked Mar 7, 2021 47.7k views

1 Answer

Jbp · Answer 1 · 2021-03-11T13:52:41+0000

Answer:

0.083 = 8.3% probability that the truck driver goes more than 475 miles in a day.

Explanation:

An uniform probability is a case of probability in which each outcome is equally as likely.

For this situation, we have a lower limit of the distribution that we call a and an upper limit that we call b.

The probability that we find a value X lower than x or equal is given by the following formula.

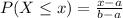
$P(X \leq x) = (x - a)/(b-a)$

The number of miles driven by a truck driver in a day falls between 200 and 500, and follows a uniform distribution.

This means that
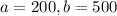
a = 200, b = 500

(a) Find the probability that the truck driver goes more than 475 miles in a day. (Round your answer to three decimal places.)

Either he goes 475 miles or lower, or he goes more than 475 miles. The sum of the probabilities of these events is 1.

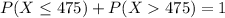
$P(X \leq 475) + P(X > 475) = 1$

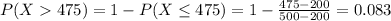
$P(X > 475) = 1 - P(X \leq 475) = 1 - (475 - 200)/(500 - 200) = 0.083$

0.083 = 8.3% probability that the truck driver goes more than 475 miles in a day.