Question

Suppose that if you arrive at a bus stop at 8:00, the number of minutes that you will have to wait for the next bus is uniformly distributed on [0,10]. a) Find the probability that you will have to wait at least six minutes for the bus. b) Find the probability that you will have to wait between two and four minutes. c) Find the expected value and standard deviation of the number of minutes that you have to wait for the next bus.

Answer 1

a) 40% probability that you will have to wait at least six minutes for the bus.

b) 20% probability that you will have to wait between two and four minutes.

c) The expeted value is 5 minutes and the standard deviation is of 2.8868 minutes.

Explanation:

An uniform probability is a case of probability in which each outcome is equally as likely.

For this situation, we have a lower limit of the distribution that we call a and an upper limit that we call b.

The probability that we find a value X lower than x is given by the following formula.

`P(X < x) = (x - a)/(b-a)`

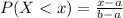
The probability that we find a value X between two values c and d, in which d is greater than c is given by the following formula:

`P(c \leq X \leq d) = (d - c)/(b-a)`

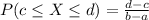
The expected value of the uniform distribution is given by:

`E = (a+b)/(2)`

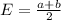
The variance of the uniform distribution is given by:

`V = ((b-a)^(2))/(12)`

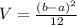
The standard deviation is the square root of the variance.

Suppose that if you arrive at a bus stop at 8:00, the number of minutes that you will have to wait for the next bus is uniformly distributed on [0,10]

This means that
`a = 0, b = 10`

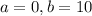
a) Find the probability that you will have to wait at least six minutes for the bus.

Either you have to wait less than 6 minutes, or you have to wait at least 6 minutes. The sum of the probabilities of these events is 1. So

`P(X < 6) + P(X \geq 6) = 1`

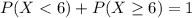
We want
`P(X \geq 6)`

`P(X \geq 6) = 1 - P(X < 6) = 1 - (6 - 0)/(10 - 0) = 0.4`

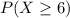
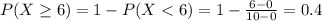
40% probability that you will have to wait at least six minutes for the bus.

b) Find the probability that you will have to wait between two and four minutes.

`P(2 \leq X \leq 4) = (4 - 2)/(10 - 0) = 0.2`

20% probability that you will have to wait between two and four minutes.

c) Find the expected value and standard deviation of the number of minutes that you have to wait for the next bus.

Expeted value:

`E = (a+b)/(2) = (0+10)/(2)`

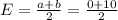
Standard deviation:

`V = ((b-a)^(2))/(12) = ((10-0)^(2))/(12) = 8.33`

`S = √(8.333) = 2.8868`

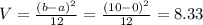
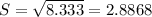
The expeted value is 5 minutes and the standard deviation is of 2.8868 minutes.