Answer:
90% confidence interval for the population mean time = [7.944 , 8.456]
Explanation:
We are given that the Bureau surveys 200 people. The sample mean is 8.2 minutes. There is a known standard deviation of 2.2 minutes.
Now, the pivotal quantity for 90% confidence interval for the population mean time to complete the forms is;
P.Q. =
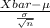 ~ N(0,1)
~ N(0,1)
where, Xbar = sample mean = 8.2 minutes
 = population standard deviation = 2.2 minutes
= population standard deviation = 2.2 minutes
n = sample size = 200
So, 90% confidence interval for the population mean time,
 is ;
is ;
P(-1.6449 < N(0,1) < 1.6449) = 0.90
P(-1.6449 <
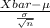 < 1.6449) = 0.90
< 1.6449) = 0.90
P(-1.6449 *
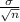 <
<
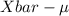 < 1.6449 *
< 1.6449 *
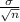 ) = 0.90
) = 0.90
P(Xbar - 1.6449 *
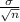 <
<
 < Xbar + 1.6449 *
< Xbar + 1.6449 *
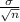 ) = 0.90
) = 0.90
90% confidence interval for
 = [Xbar - 1.6449 *
= [Xbar - 1.6449 *
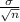 , Xbar + 1.6449 *
, Xbar + 1.6449 *
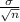 ]
]
= [8.2 - 1.6449 *
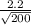 , 8.2 + 1.6449 *
, 8.2 + 1.6449 *
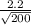 ]
]
= [7.944 , 8.456]
Therefore, 90% confidence interval for the population mean time to complete the forms is [7.944 , 8.456] .